 Symmetry adapted modes
Symmetry adapted modes
 Online Help
Online Help
Bilbao Crystallographic Server
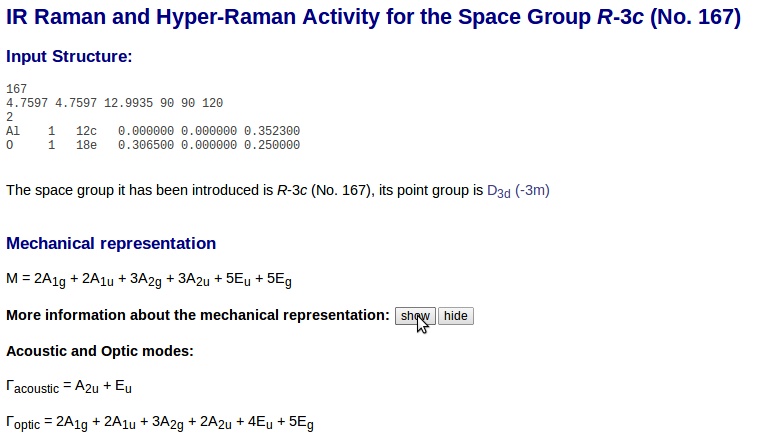
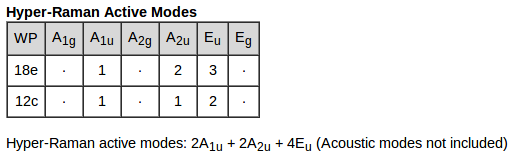
 Symmetry adapted modes
Symmetry adapted modes
 Online Help Online Help
|

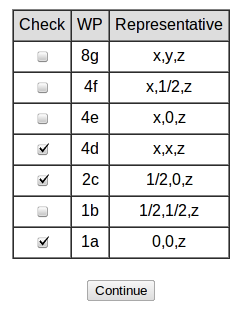
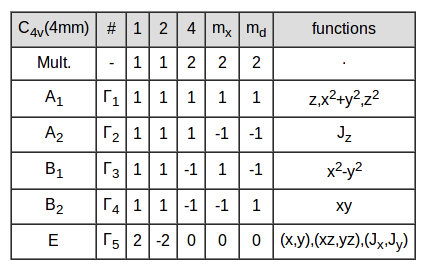
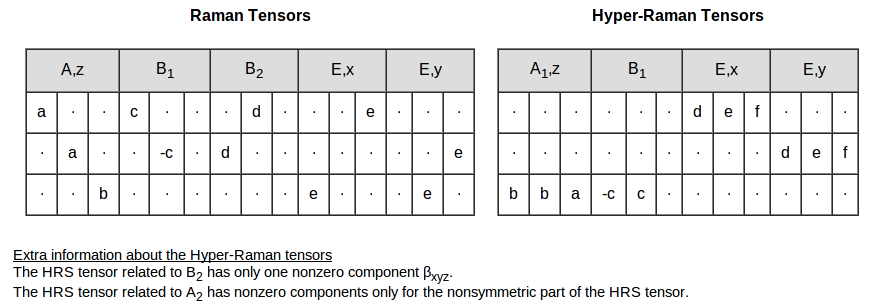
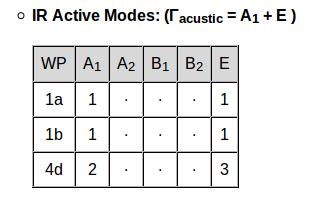 |
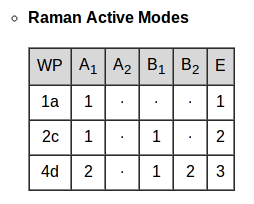 |
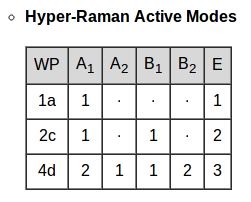 |
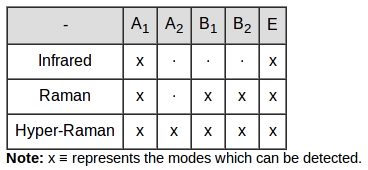
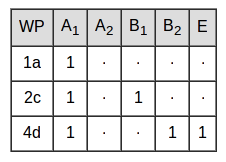
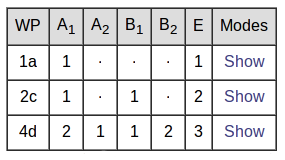
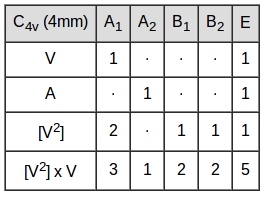
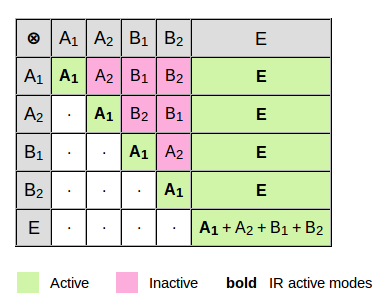
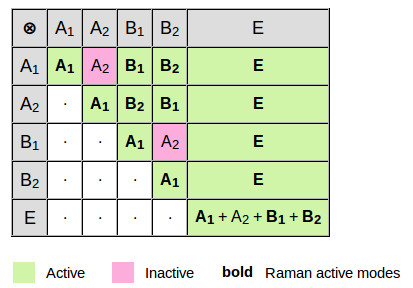

|

|
|
|
http://www.cryst.ehu.es
Bilbao Crystallographic Server |
For comments, please mail to
cryst@wm.lc.ehu.es |