Case Study: Group - Subgroup Transition of BaTiO3
Contents
Case Study: Group - Subgroup Transition of BaTiO3¶
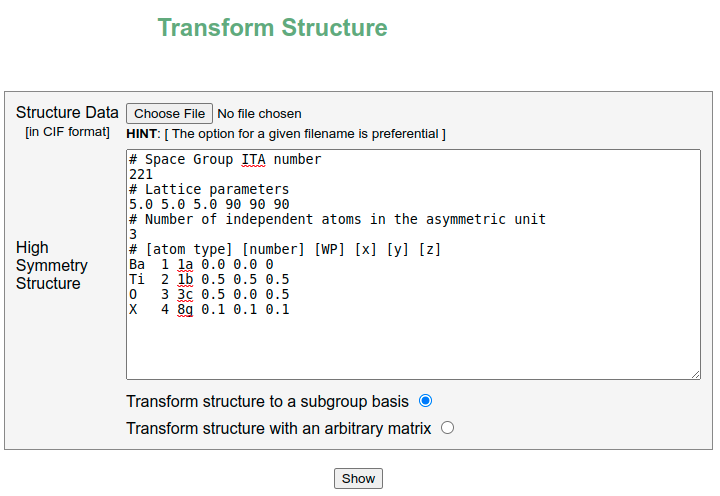
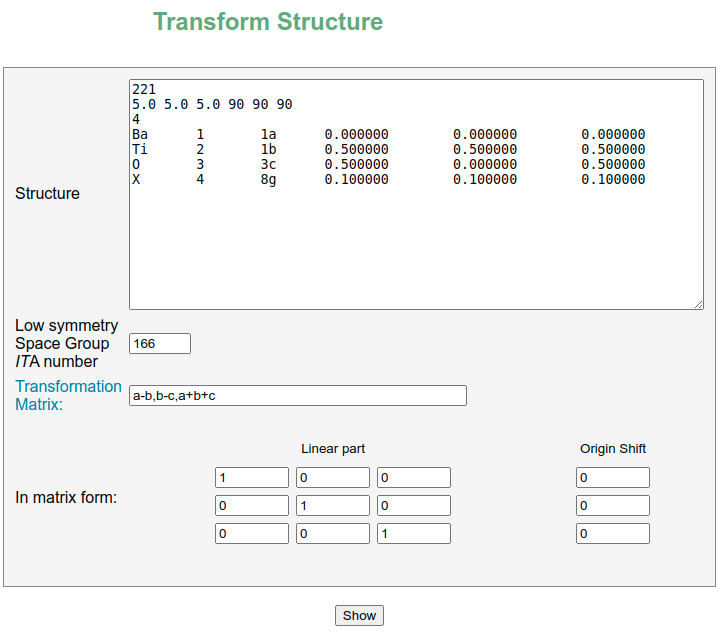
We will start from the cubic BaTiO3 given in the Pm3m (#221) space group setting and will tranform it to the R3m (#166) space group setting via the transformation matrix: \(P=a-b,b-c,a+b+c\).
We have already covered this case partially in the Transformations chapter and here we will have it done from A to Z.
The structure data of BaTiO3 is given in BCS format as:
221
5.0 5.0 5.0 90 90 90
3
Ba 1 1a 0.000000 0.000000 0.000000
Ti 2 1b 0.500000 0.500000 0.500000
O 3 3c 0.500000 0.000000 0.500000
and its CIF file can be downloaded here: BaTiO3_221.cif
Transformation of the Lattice Parameters¶
As we have seen in the transformations chapter, under the given transformation, the unit cell changes its shape from the cubic phase:
5.0 5.0 5.0 90 90 90
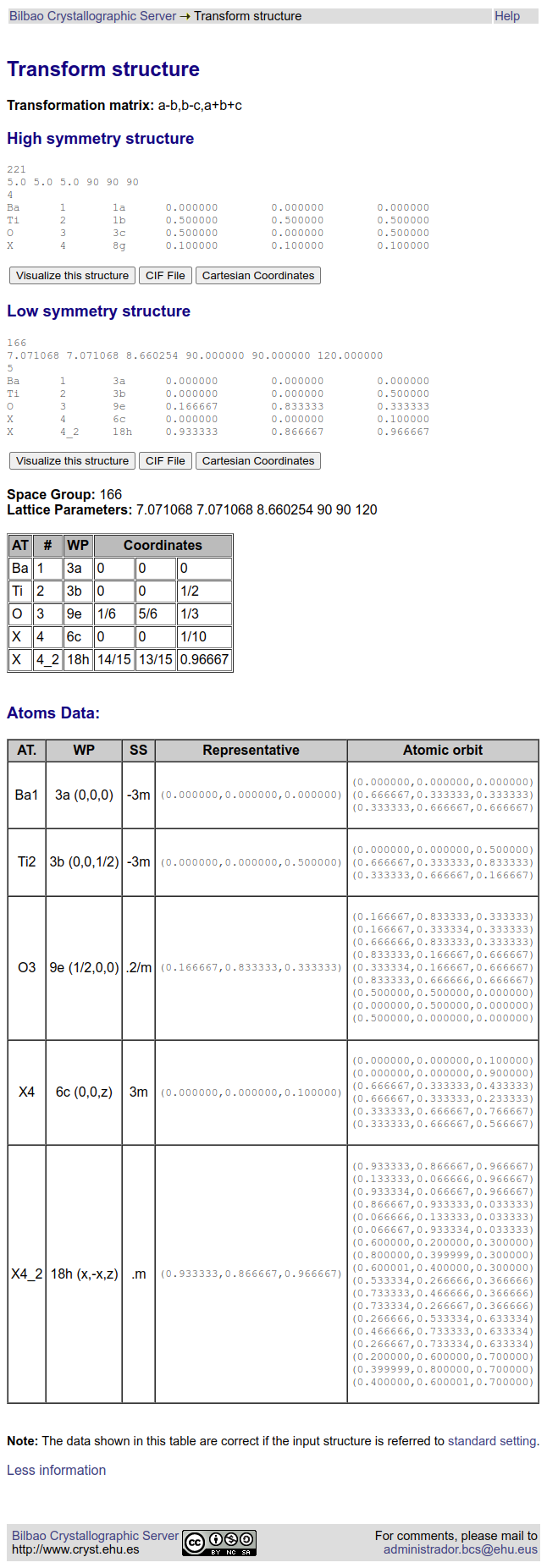
to the hexagonal phase:
7.071068 7.071068 8.660254 90.0 90.0 120.0
The hexagonal phase’s parameters are calculated by transforming the metric tensor.
import numpy as np
def metric_from_vector(vec):
# Constructs the metric tensor from the input lattice vectors
# Vectors are input as a 3x3, with each lattice vector given
# as a row-vector
# Returns the metric tensor as a 3x3 matrix
G = np.empty((3,3))
for i in range(3):
for j in range(i,3):
G[i,j] = G[j,i] = np.dot(vec[i,:],vec[j,:])
return G
def parameters_from_metric(G):
a = np.sqrt(G[0,0])
b = np.sqrt(G[1,1])
c = np.sqrt(G[2,2])
alpha = np.rad2deg(np.arccos(G[1,2]/(b*c)))
beta = np.rad2deg(np.arccos(G[0,2]/(a*c)))
gamma = np.rad2deg(np.arccos(G[0,1]/(a*b)))
return np.array([a,b,c,alpha,beta,gamma])
def par2vec(par):
# Converts from parametric form to vectorial form
# Lattice parameters are input as a 6 dimensional vector
# Returns the lattice vectors as a 3x3 matrix, with each
# vector as a row-vector
a = par[0]
b = par[1]
c = par[2]
alpha = np.deg2rad(par[3])
beta = np.deg2rad(par[4])
gamma = np.deg2rad(par[5])
a1 = a
vec_a = np.array([a1,0,0])
b1 = b*np.cos(gamma)
b2 = np.sqrt(b**2 - b1**2)
vec_b = np.array([b1,b2,0])
c1 = c*np.cos(beta)
c2 = ((b*c*np.cos(alpha))- b1*c1)/b2
c3 = np.sqrt(c**2 - c1**2 - c2**2)
vec_c = np.array([c1,c2,c3])
abc_vec = np.array([vec_a,vec_b,vec_c])
return abc_vec
par_221 = np.array([5.,5,5,90,90,90])
vec_221 = par2vec(par_221)
G_221 = metric_from_vector(vec_221)
P = np.array([[1,0,1],\
[-1,1,1],\
[0,-1,1]])
G_166 = np.linalg.multi_dot((P.T,G_221,P))
par_166 = parameters_from_metric(G_166)
print(("{:.4f} "*3+"{:.2f} "*3).format(*par_166))
7.0711 7.0711 8.6603 90.00 90.00 120.00
Comparing the volumes, we see that, in the subgroup setting, the unit cell is 3 times greater in volume than the supergroup setting:
volume_221 = np.sqrt(np.linalg.det(G_221))
volume_166 = np.sqrt(np.linalg.det(G_166))
print("The volume of the unit cell in #221 setting: {:.2f} ų"\
.format(volume_221))
print("The volume of the unit cell in #166 setting: {:.2f} ų"\
.format(volume_166))
print(" Ratio of the volumes: {:.2f}/{:.2f} = {:.2f}"\
.format(volume_166,volume_221,volume_166/volume_221))
The volume of the unit cell in #221 setting: 125.00 ų
The volume of the unit cell in #166 setting: 375.00 ų
Ratio of the volumes: 375.00/125.00 = 3.00
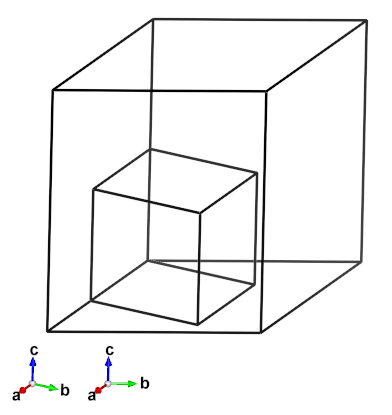
The change in volume automatically implies that the number of atoms per unit cell will also change. In our case, we had 5 atoms in our cubic unit cell but in the supergroup we’ll have 5x3=15 atoms. This is not something like “atoms appearing out of nowhere” – we are simply expanding the dimensions of our unit cell to comply with the subgroup settings.
Transformation of the Symmetry Operators¶
Pm3m (#221) space group contains 48 symmetry operators and given in xyz notation, they are:
x,y,z |
-x,-y,z |
-x,y,-z |
x,-y,-z |
z,x,y |
z,-x,-y |
-z,-x,y |
-z,x,-y |
y,z,x |
-y,z,-x |
y,-z,-x |
-y,-z,x |
y,x,-z |
-y,-x,-z |
y,-x,z |
-y,x,z |
x,z,-y |
-x,z,y |
-x,-z,-y |
x,-z,y |
z,y,-x |
z,-y,x |
-z,y,x |
-z,-y,-x |
-x,-y,-z |
x,y,-z |
x,-y,z |
-x,y,z |
-z,-x,-y |
-z,x,y |
z,x,-y |
z,-x,y |
-y,-z,-x |
y,-z,x |
-y,z,x |
y,z,-x |
-y,-x,z |
y,x,z |
-y,x,-z |
y,-x,-z |
-x,-z,y |
x,-z,-y |
x,z,y |
-x,z,-y |
-z,-y,x |
-z,y,-x |
z,-y,-x |
z,y,x |
The cell below contains the definition of the labels of the symmetry operators:
labels = []
labels.append("1 || x,y,z")
labels.append("2 0,0,z || -x,-y,z")
labels.append("2 0,y,0 || -x,y,-z")
labels.append("2 x,0,0 || x,-y,-z")
labels.append("3- x,x,x || z,x,y")
labels.append("3- -x,x,-x || z,-x,-y")
labels.append("3- x,-x,-x || -z,-x,y")
labels.append("3- -x,-x,x || -z,x,-y")
labels.append("3+ x,x,x || y,z,x")
labels.append("3+ x,-x,-x || -y,z,-x")
labels.append("3+ -x,-x,x || y,-z,-x")
labels.append("3+ -x,x,-x || -y,-z,x")
labels.append("2 x,x,0 || y,x,-z")
labels.append("2 x,-x,0 || -y,-x,-z")
labels.append("4+ 0,0,z || y,-x,z")
labels.append("4- 0,0,z || -y,x,z")
labels.append("4+ x,0,0 || x,z,-y")
labels.append("2 0,y,y || -x,z,y")
labels.append("2 0,y,-y || -x,-z,-y")
labels.append("4- x,0,0 || x,-z,y")
labels.append("4- 0,y,0 || z,y,-x")
labels.append("2 x,0,x || z,-y,x")
labels.append("4+ 0,y,0 || -z,y,x")
labels.append("2 -x,0,x || -z,-y,-x")
labels.append("-1 0,0,0 || -x,-y,-z")
labels.append("m x,y,0 || x,y,-z")
labels.append("m x,0,z || x,-y,z")
labels.append("m 0,y,z || -x,y,z")
labels.append("-3- x,x,x; 0,0,0 || -z,-x,-y")
labels.append("-3- -x,x,-x; 0,0,0 || -z,x,y")
labels.append("-3- x,-x,-x; 0,0,0 || z,x,-y")
labels.append("-3- -x,-x,x; 0,0,0 || z,-x,y")
labels.append("-3+ x,x,x; 0,0,0 || -y,-z,-x")
labels.append("-3+ x,-x,-x; 0,0,0 || y,-z,x")
labels.append("-3+ -x,-x,x; 0,0,0 || -y,z,x")
labels.append("-3+ -x,x,-x; 0,0,0 || y,z,-x")
labels.append("m x,-x,z || -y,-x,z")
labels.append("m x,x,z || y,x,z")
labels.append("-4+ 0,0,z; 0,0,0 || -y,x,-z")
labels.append("-4- 0,0,z; 0,0,0 || y,-x,-z")
labels.append("-4+ x,0,0; 0,0,0 || -x,-z,y")
labels.append("m x,y,-y || x,-z,-y")
labels.append("m x,y,y || x,z,y")
labels.append("-4- x,0,0; 0,0,0 || -x,z,-y")
labels.append("-4- 0,y,0; 0,0,0 || -z,-y,x")
labels.append("m -x,y,x || -z,y,-x")
labels.append("-4+ 0,y,0; 0,0,0 || z,-y,-x")
labels.append("m x,y,x || z,y,x")
labels
['1 || x,y,z',
'2 0,0,z || -x,-y,z',
'2 0,y,0 || -x,y,-z',
'2 x,0,0 || x,-y,-z',
'3- x,x,x || z,x,y',
'3- -x,x,-x || z,-x,-y',
'3- x,-x,-x || -z,-x,y',
'3- -x,-x,x || -z,x,-y',
'3+ x,x,x || y,z,x',
'3+ x,-x,-x || -y,z,-x',
'3+ -x,-x,x || y,-z,-x',
'3+ -x,x,-x || -y,-z,x',
'2 x,x,0 || y,x,-z',
'2 x,-x,0 || -y,-x,-z',
'4+ 0,0,z || y,-x,z',
'4- 0,0,z || -y,x,z',
'4+ x,0,0 || x,z,-y',
'2 0,y,y || -x,z,y',
'2 0,y,-y || -x,-z,-y',
'4- x,0,0 || x,-z,y',
'4- 0,y,0 || z,y,-x',
'2 x,0,x || z,-y,x',
'4+ 0,y,0 || -z,y,x',
'2 -x,0,x || -z,-y,-x',
'-1 0,0,0 || -x,-y,-z',
'm x,y,0 || x,y,-z',
'm x,0,z || x,-y,z',
'm 0,y,z || -x,y,z',
'-3- x,x,x; 0,0,0 || -z,-x,-y',
'-3- -x,x,-x; 0,0,0 || -z,x,y',
'-3- x,-x,-x; 0,0,0 || z,x,-y',
'-3- -x,-x,x; 0,0,0 || z,-x,y',
'-3+ x,x,x; 0,0,0 || -y,-z,-x',
'-3+ x,-x,-x; 0,0,0 || y,-z,x',
'-3+ -x,-x,x; 0,0,0 || -y,z,x',
'-3+ -x,x,-x; 0,0,0 || y,z,-x',
'm x,-x,z || -y,-x,z',
'm x,x,z || y,x,z',
'-4+ 0,0,z; 0,0,0 || -y,x,-z',
'-4- 0,0,z; 0,0,0 || y,-x,-z',
'-4+ x,0,0; 0,0,0 || -x,-z,y',
'm x,y,-y || x,-z,-y',
'm x,y,y || x,z,y',
'-4- x,0,0; 0,0,0 || -x,z,-y',
'-4- 0,y,0; 0,0,0 || -z,-y,x',
'm -x,y,x || -z,y,-x',
'-4+ 0,y,0; 0,0,0 || z,-y,-x',
'm x,y,x || z,y,x']
The cell below contains the definitions of the matrix representations of the symmetry operators:
ops = []
ops.append(np.array([[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops.append(np.array([[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
ops
[array([[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]]),
array([[-1., 0., 0., 0.],
[ 0., -1., 0., 0.],
[ 0., 0., 1., 0.],
[ 0., 0., 0., 1.]]),
array([[-1., 0., 0., 0.],
[ 0., 1., 0., 0.],
[ 0., 0., -1., 0.],
[ 0., 0., 0., 1.]]),
array([[ 1., 0., 0., 0.],
[ 0., -1., 0., 0.],
[ 0., 0., -1., 0.],
[ 0., 0., 0., 1.]]),
array([[0., 0., 1., 0.],
[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 0., 1.]]),
array([[ 0., 0., 1., 0.],
[-1., 0., 0., 0.],
[ 0., -1., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., 0., -1., 0.],
[-1., 0., 0., 0.],
[ 0., 1., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., 0., -1., 0.],
[ 1., 0., 0., 0.],
[ 0., -1., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[0., 1., 0., 0.],
[0., 0., 1., 0.],
[1., 0., 0., 0.],
[0., 0., 0., 1.]]),
array([[ 0., -1., 0., 0.],
[ 0., 0., 1., 0.],
[-1., 0., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., 1., 0., 0.],
[ 0., 0., -1., 0.],
[-1., 0., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., -1., 0., 0.],
[ 0., 0., -1., 0.],
[ 1., 0., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., 1., 0., 0.],
[ 1., 0., 0., 0.],
[ 0., 0., -1., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., -1., 0., 0.],
[-1., 0., 0., 0.],
[ 0., 0., -1., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., 1., 0., 0.],
[-1., 0., 0., 0.],
[ 0., 0., 1., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., -1., 0., 0.],
[ 1., 0., 0., 0.],
[ 0., 0., 1., 0.],
[ 0., 0., 0., 1.]]),
array([[ 1., 0., 0., 0.],
[ 0., 0., 1., 0.],
[ 0., -1., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[-1., 0., 0., 0.],
[ 0., 0., 1., 0.],
[ 0., 1., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[-1., 0., 0., 0.],
[ 0., 0., -1., 0.],
[ 0., -1., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 1., 0., 0., 0.],
[ 0., 0., -1., 0.],
[ 0., 1., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., 0., 1., 0.],
[ 0., 1., 0., 0.],
[-1., 0., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., 0., 1., 0.],
[ 0., -1., 0., 0.],
[ 1., 0., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., 0., -1., 0.],
[ 0., 1., 0., 0.],
[ 1., 0., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., 0., -1., 0.],
[ 0., -1., 0., 0.],
[-1., 0., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[-1., 0., 0., 0.],
[ 0., -1., 0., 0.],
[ 0., 0., -1., 0.],
[ 0., 0., 0., 1.]]),
array([[ 1., 0., 0., 0.],
[ 0., 1., 0., 0.],
[ 0., 0., -1., 0.],
[ 0., 0., 0., 1.]]),
array([[ 1., 0., 0., 0.],
[ 0., -1., 0., 0.],
[ 0., 0., 1., 0.],
[ 0., 0., 0., 1.]]),
array([[-1., 0., 0., 0.],
[ 0., 1., 0., 0.],
[ 0., 0., 1., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., 0., -1., 0.],
[-1., 0., 0., 0.],
[ 0., -1., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., 0., -1., 0.],
[ 1., 0., 0., 0.],
[ 0., 1., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., 0., 1., 0.],
[ 1., 0., 0., 0.],
[ 0., -1., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., 0., 1., 0.],
[-1., 0., 0., 0.],
[ 0., 1., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., -1., 0., 0.],
[ 0., 0., -1., 0.],
[-1., 0., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., 1., 0., 0.],
[ 0., 0., -1., 0.],
[ 1., 0., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., -1., 0., 0.],
[ 0., 0., 1., 0.],
[ 1., 0., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., 1., 0., 0.],
[ 0., 0., 1., 0.],
[-1., 0., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., -1., 0., 0.],
[-1., 0., 0., 0.],
[ 0., 0., 1., 0.],
[ 0., 0., 0., 1.]]),
array([[0., 1., 0., 0.],
[1., 0., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]]),
array([[ 0., -1., 0., 0.],
[ 1., 0., 0., 0.],
[ 0., 0., -1., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., 1., 0., 0.],
[-1., 0., 0., 0.],
[ 0., 0., -1., 0.],
[ 0., 0., 0., 1.]]),
array([[-1., 0., 0., 0.],
[ 0., 0., -1., 0.],
[ 0., 1., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 1., 0., 0., 0.],
[ 0., 0., -1., 0.],
[ 0., -1., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[1., 0., 0., 0.],
[0., 0., 1., 0.],
[0., 1., 0., 0.],
[0., 0., 0., 1.]]),
array([[-1., 0., 0., 0.],
[ 0., 0., 1., 0.],
[ 0., -1., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., 0., -1., 0.],
[ 0., -1., 0., 0.],
[ 1., 0., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., 0., -1., 0.],
[ 0., 1., 0., 0.],
[-1., 0., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[ 0., 0., 1., 0.],
[ 0., -1., 0., 0.],
[-1., 0., 0., 0.],
[ 0., 0., 0., 1.]]),
array([[0., 0., 1., 0.],
[0., 1., 0., 0.],
[1., 0., 0., 0.],
[0., 0., 0., 1.]])]
Here are the first three operators, to give an idea:
for i in range(3):
print("Label & xyz: ",labels[i])
print(ops[i])
print("-"*30)
Label & xyz: 1 || x,y,z
[[1. 0. 0. 0.]
[0. 1. 0. 0.]
[0. 0. 1. 0.]
[0. 0. 0. 1.]]
------------------------------
Label & xyz: 2 0,0,z || -x,-y,z
[[-1. 0. 0. 0.]
[ 0. -1. 0. 0.]
[ 0. 0. 1. 0.]
[ 0. 0. 0. 1.]]
------------------------------
Label & xyz: 2 0,y,0 || -x,y,-z
[[-1. 0. 0. 0.]
[ 0. 1. 0. 0.]
[ 0. 0. -1. 0.]
[ 0. 0. 0. 1.]]
------------------------------
Now that we have the operators, we can transform them accordingly with the operator transformation formula:
P = np.array([[1,0,1,0],\
[-1,1,1,0],\
[0,-1,1,0],\
[0,0,0,1]])
P_inv = np.linalg.inv(P)
ops_transformed = []
for t in range(1):
for i in range(len(ops)):
op = ops[i]
op_transformed = np.linalg.multi_dot((P_inv,op,P))
op_transformed[np.abs(op_transformed)<1E-15] = 0
# Check if the transformed operators has already been acquired
flag_not_found_before = True
for j in range(len(ops_transformed)):
if(np.allclose(op_transformed,ops_transformed[j])):
flag_not_found_before = False
break
if(flag_not_found_before):
ops_transformed.append(op_transformed)
len(ops_transformed)
48
for (i,op) in enumerate(ops_transformed,start=1):
print(("{:2d}\n"+("{:8.4f} "*4+"\n")*4).format(i,*op.flatten()))
1
1.0000 0.0000 0.0000 0.0000
0.0000 1.0000 0.0000 0.0000
0.0000 0.0000 1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
2
-1.0000 0.6667 -0.6667 0.0000
0.0000 0.3333 -1.3333 0.0000
0.0000 -0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
3
-0.3333 -0.6667 -0.6667 0.0000
-0.6667 -0.3333 0.6667 0.0000
-0.6667 0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
4
0.3333 0.0000 1.3333 0.0000
0.6667 -1.0000 0.6667 0.0000
0.6667 0.0000 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
5
0.0000 -1.0000 0.0000 0.0000
1.0000 -1.0000 0.0000 0.0000
0.0000 0.0000 1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
6
0.0000 -0.3333 1.3333 0.0000
-1.0000 0.3333 0.6667 0.0000
0.0000 -0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
7
0.6667 0.3333 -0.6667 0.0000
0.3333 -0.3333 -1.3333 0.0000
-0.6667 0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
8
-0.6667 1.0000 -0.6667 0.0000
-0.3333 1.0000 0.6667 0.0000
0.6667 0.0000 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
9
-1.0000 1.0000 0.0000 0.0000
-1.0000 0.0000 0.0000 0.0000
0.0000 0.0000 1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
10
1.0000 -0.3333 -0.6667 0.0000
1.0000 -0.6667 0.6667 0.0000
0.0000 -0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
11
-0.3333 0.3333 1.3333 0.0000
0.3333 0.6667 0.6667 0.0000
-0.6667 0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
12
0.3333 -1.0000 -0.6667 0.0000
-0.3333 0.0000 -1.3333 0.0000
0.6667 0.0000 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
13
-1.0000 0.3333 0.6667 0.0000
0.0000 -0.3333 1.3333 0.0000
0.0000 0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
14
1.0000 -1.0000 0.0000 0.0000
0.0000 -1.0000 0.0000 0.0000
0.0000 0.0000 -1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
15
-0.3333 1.0000 0.6667 0.0000
-0.6667 1.0000 -0.6667 0.0000
-0.6667 0.0000 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
16
0.3333 -0.3333 -1.3333 0.0000
0.6667 0.3333 -0.6667 0.0000
0.6667 -0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
17
0.3333 0.6667 0.6667 0.0000
-0.3333 0.3333 1.3333 0.0000
0.6667 -0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
18
-0.3333 0.0000 -1.3333 0.0000
0.3333 -1.0000 -0.6667 0.0000
-0.6667 0.0000 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
19
-1.0000 0.0000 0.0000 0.0000
-1.0000 1.0000 0.0000 0.0000
0.0000 0.0000 -1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
20
1.0000 -0.6667 0.6667 0.0000
1.0000 -0.3333 -0.6667 0.0000
0.0000 0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
21
0.6667 -1.0000 0.6667 0.0000
0.3333 0.0000 1.3333 0.0000
-0.6667 0.0000 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
22
-0.6667 -0.3333 0.6667 0.0000
-0.3333 -0.6667 -0.6667 0.0000
0.6667 -0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
23
0.0000 0.3333 -1.3333 0.0000
-1.0000 0.6667 -0.6667 0.0000
0.0000 0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
24
0.0000 1.0000 0.0000 0.0000
1.0000 0.0000 0.0000 0.0000
0.0000 0.0000 -1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
25
-1.0000 0.0000 0.0000 0.0000
0.0000 -1.0000 0.0000 0.0000
0.0000 0.0000 -1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
26
1.0000 -0.6667 0.6667 0.0000
0.0000 -0.3333 1.3333 0.0000
0.0000 0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
27
0.3333 0.6667 0.6667 0.0000
0.6667 0.3333 -0.6667 0.0000
0.6667 -0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
28
-0.3333 0.0000 -1.3333 0.0000
-0.6667 1.0000 -0.6667 0.0000
-0.6667 0.0000 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
29
0.0000 1.0000 0.0000 0.0000
-1.0000 1.0000 0.0000 0.0000
0.0000 0.0000 -1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
30
0.0000 0.3333 -1.3333 0.0000
1.0000 -0.3333 -0.6667 0.0000
0.0000 0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
31
-0.6667 -0.3333 0.6667 0.0000
-0.3333 0.3333 1.3333 0.0000
0.6667 -0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
32
0.6667 -1.0000 0.6667 0.0000
0.3333 -1.0000 -0.6667 0.0000
-0.6667 0.0000 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
33
1.0000 -1.0000 0.0000 0.0000
1.0000 0.0000 0.0000 0.0000
0.0000 0.0000 -1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
34
-1.0000 0.3333 0.6667 0.0000
-1.0000 0.6667 -0.6667 0.0000
0.0000 0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
35
0.3333 -0.3333 -1.3333 0.0000
-0.3333 -0.6667 -0.6667 0.0000
0.6667 -0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
36
-0.3333 1.0000 0.6667 0.0000
0.3333 0.0000 1.3333 0.0000
-0.6667 0.0000 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
37
1.0000 -0.3333 -0.6667 0.0000
0.0000 0.3333 -1.3333 0.0000
0.0000 -0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
38
-1.0000 1.0000 0.0000 0.0000
0.0000 1.0000 0.0000 0.0000
0.0000 0.0000 1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
39
0.3333 -1.0000 -0.6667 0.0000
0.6667 -1.0000 0.6667 0.0000
0.6667 0.0000 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
40
-0.3333 0.3333 1.3333 0.0000
-0.6667 -0.3333 0.6667 0.0000
-0.6667 0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
41
-0.3333 -0.6667 -0.6667 0.0000
0.3333 -0.3333 -1.3333 0.0000
-0.6667 0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
42
0.3333 0.0000 1.3333 0.0000
-0.3333 1.0000 0.6667 0.0000
0.6667 0.0000 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
43
1.0000 0.0000 0.0000 0.0000
1.0000 -1.0000 0.0000 0.0000
0.0000 0.0000 1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
44
-1.0000 0.6667 -0.6667 0.0000
-1.0000 0.3333 0.6667 0.0000
0.0000 -0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
45
-0.6667 1.0000 -0.6667 0.0000
-0.3333 0.0000 -1.3333 0.0000
0.6667 0.0000 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
46
0.6667 0.3333 -0.6667 0.0000
0.3333 0.6667 0.6667 0.0000
-0.6667 0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
47
0.0000 -0.3333 1.3333 0.0000
1.0000 -0.6667 0.6667 0.0000
0.0000 -0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
48
0.0000 -1.0000 0.0000 0.0000
-1.0000 0.0000 0.0000 0.0000
0.0000 0.0000 1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
We could as well have used GENPOS (with the “User-Defined Setting” option defined) to retrieve the list under our transformation:

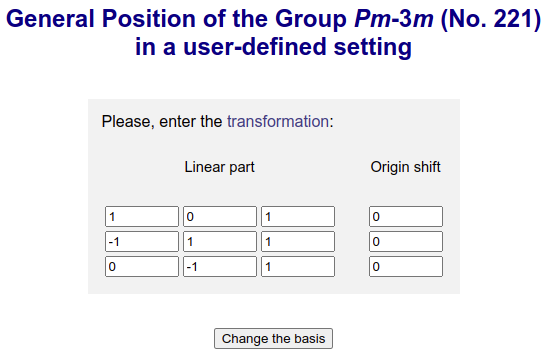

At this point, we are missing an important thing: due to periodicity, a space group actually has an infinite number of symmetry operators (remember the lattice translation operators!). Normally, as we were operating within our unit cell, the lattice translation operators were taking us from one unit cell to an equivalent site in an another unit cell however, now that our unit cell dimensions have changed, we also need to check how our lattice translation operators behave in the subgroup setting:
op_trans_a = np.eye(4,4)
op_trans_b = np.eye(4,4)
op_trans_c = np.eye(4,4)
op_trans_a[:3,3] = np.array([1,0,0])
op_trans_b[:3,3] = np.array([1,1,0])
op_trans_c[:3,3] = np.array([1,1,1])
ops_trans = [op_trans_a, op_trans_b, op_trans_c]
for op_trans in ops_trans:
#print(op_trans)
op_transformed = np.linalg.multi_dot((P_inv,op_trans,P))
op_transformed[np.abs(op_transformed)<1E-15] = 0
op_transformed[:3,3] -= np.floor(op_transformed[:3,3])
print(op_transformed)
[[1. 0. 0. 0.66666667]
[0. 1. 0. 0.33333333]
[0. 0. 1. 0.33333333]
[0. 0. 0. 1. ]]
[[1. 0. 0. 0.33333333]
[0. 1. 0. 0.66666667]
[0. 0. 1. 0.66666667]
[0. 0. 0. 1. ]]
[[1. 0. 0. 0.]
[0. 1. 0. 0.]
[0. 0. 1. 0.]
[0. 0. 0. 1.]]
As our high symmetry cell is cubic, all the 3 directions \((a,b,c)\) are equivalent, so the lattice translation operators along these directions would transform into the same translation operator in the hexagonal unit cell. Therefore we also check their combinations along the face and body diagonals to acquire the translations in the rhombohedral R3m (#166) space group.
Symmetry Operators of the the R3m (#166) space group¶
Going from a higher symmetry group to a lower one is an indication of a symmetry break, meaning that one or more symmetry elements supported by the high symmetry structure are no longer present in the lower unit cell. But as we have seen in the structure chapter, as we loose symmetries, we are loosing the connections between sites, such that the orbits are splitting (we will deal with this later in this chapter).
We have seen that, apart from the lattice translation operators, the Pm3m (#221) contained 48 symmetry operators. The lower symmetry space group R3m (#166) contains the following 36 symmetry operators:
x,y,z |
-y,x-y,z |
-x+y,-x,z |
y,x,-z |
x-y,-y,-z |
-x,-x+y,-z |
-x,-y,-z |
y,-x+y,-z |
x-y,x,-z |
-y,-x,z |
-x+y,y,z |
x,x-y,z |
x+2/3,y+1/3,z+1/3 |
-y+2/3,x-y+1/3,z+1/3 |
-x+y+2/3,-x+1/3,z+1/3 |
y+2/3,x+1/3,-z+1/3 |
x-y+2/3,-y+1/3,-z+1/3 |
-x+2/3,-x+y+1/3,-z+1/3 |
-x+2/3,-y+1/3,-z+1/3 |
y+2/3,-x+y+1/3,-z+1/3 |
x-y+2/3,x+1/3,-z+1/3 |
-y+2/3,-x+1/3,z+1/3 |
-x+y+2/3,y+1/3,z+1/3 |
x+2/3,x-y+1/3,z+1/3 |
x+1/3,y+2/3,z+2/3 |
-y+1/3,x-y+2/3,z+2/3 |
-x+y+1/3,-x+2/3,z+2/3 |
y+1/3,x+2/3,-z+2/3 |
x-y+1/3,-y+2/3,-z+2/3 |
-x+1/3,-x+y+2/3,-z+2/3 |
-x+1/3,-y+2/3,-z+2/3 |
y+1/3,-x+y+2/3,-z+2/3 |
x-y+1/3,x+2/3,-z+2/3 |
-y+1/3,-x+2/3,z+2/3 |
-x+y+1/3,y+2/3,z+2/3 |
x+1/3,x-y+2/3,z+2/3 |
Checking them, we see that the first 12 operators are repeated with the translations \(\{1|2/3,1/3,1/3\}\) and \(\{1|1/3,2/3,2/3\}\) applied to them.
Taking a wide range of operators of the high symmetry group and transforming them accordingly with the:
and then fixing the translational parts to be withing \([0,1)\), we end up with 144 distinct operators:
ops_p = []
for t_x in range(3):
for t_y in range(3):
for t_z in range(3):
translation = np.zeros((4,4))
translation[0,3] = t_x
translation[1,3] = t_y
translation[2,3] = t_z
translation[3,3] = 0
for opy in ops:
op0 = opy.copy()
op0 += translation
op = np.linalg.multi_dot((P_inv,op0,P))
op[:3,3] -= np.floor(op[:3,3])
flag_not_found = True
for i in ops_p:
if(np.allclose(op,i)):
flag_not_found = False
break
if(flag_not_found):
ops_p.append(op)
for (i,op) in enumerate(ops_p,start=1):
print(("{:2d}\n"+("{:8.4f} "*4+"\n")*4).format(i,*op.flatten()))
1
1.0000 0.0000 0.0000 0.0000
0.0000 1.0000 0.0000 0.0000
0.0000 0.0000 1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
2
-1.0000 0.6667 -0.6667 0.0000
0.0000 0.3333 -1.3333 0.0000
0.0000 -0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
3
-0.3333 -0.6667 -0.6667 0.0000
-0.6667 -0.3333 0.6667 0.0000
-0.6667 0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
4
0.3333 0.0000 1.3333 0.0000
0.6667 -1.0000 0.6667 0.0000
0.6667 0.0000 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
5
0.0000 -1.0000 0.0000 0.0000
1.0000 -1.0000 0.0000 0.0000
0.0000 0.0000 1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
6
0.0000 -0.3333 1.3333 0.0000
-1.0000 0.3333 0.6667 0.0000
0.0000 -0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
7
0.6667 0.3333 -0.6667 0.0000
0.3333 -0.3333 -1.3333 0.0000
-0.6667 0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
8
-0.6667 1.0000 -0.6667 0.0000
-0.3333 1.0000 0.6667 0.0000
0.6667 0.0000 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
9
-1.0000 1.0000 0.0000 0.0000
-1.0000 0.0000 0.0000 0.0000
0.0000 0.0000 1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
10
1.0000 -0.3333 -0.6667 0.0000
1.0000 -0.6667 0.6667 0.0000
0.0000 -0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
11
-0.3333 0.3333 1.3333 0.0000
0.3333 0.6667 0.6667 0.0000
-0.6667 0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
12
0.3333 -1.0000 -0.6667 0.0000
-0.3333 0.0000 -1.3333 0.0000
0.6667 0.0000 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
13
-1.0000 0.3333 0.6667 0.0000
0.0000 -0.3333 1.3333 0.0000
0.0000 0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
14
1.0000 -1.0000 -0.0000 0.0000
0.0000 -1.0000 -0.0000 0.0000
0.0000 0.0000 -1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
15
-0.3333 1.0000 0.6667 0.0000
-0.6667 1.0000 -0.6667 0.0000
-0.6667 0.0000 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
16
0.3333 -0.3333 -1.3333 0.0000
0.6667 0.3333 -0.6667 0.0000
0.6667 -0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
17
0.3333 0.6667 0.6667 0.0000
-0.3333 0.3333 1.3333 0.0000
0.6667 -0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
18
-0.3333 0.0000 -1.3333 0.0000
0.3333 -1.0000 -0.6667 0.0000
-0.6667 0.0000 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
19
-1.0000 0.0000 -0.0000 0.0000
-1.0000 1.0000 -0.0000 0.0000
0.0000 0.0000 -1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
20
1.0000 -0.6667 0.6667 0.0000
1.0000 -0.3333 -0.6667 0.0000
0.0000 0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
21
0.6667 -1.0000 0.6667 0.0000
0.3333 0.0000 1.3333 0.0000
-0.6667 0.0000 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
22
-0.6667 -0.3333 0.6667 0.0000
-0.3333 -0.6667 -0.6667 0.0000
0.6667 -0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
23
0.0000 0.3333 -1.3333 0.0000
-1.0000 0.6667 -0.6667 0.0000
0.0000 0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
24
0.0000 1.0000 -0.0000 0.0000
1.0000 0.0000 -0.0000 0.0000
0.0000 0.0000 -1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
25
-1.0000 0.0000 -0.0000 0.0000
0.0000 -1.0000 -0.0000 0.0000
0.0000 0.0000 -1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
26
1.0000 -0.6667 0.6667 0.0000
0.0000 -0.3333 1.3333 0.0000
0.0000 0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
27
0.3333 0.6667 0.6667 0.0000
0.6667 0.3333 -0.6667 0.0000
0.6667 -0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
28
-0.3333 0.0000 -1.3333 0.0000
-0.6667 1.0000 -0.6667 0.0000
-0.6667 0.0000 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
29
0.0000 1.0000 -0.0000 0.0000
-1.0000 1.0000 -0.0000 0.0000
0.0000 0.0000 -1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
30
0.0000 0.3333 -1.3333 0.0000
1.0000 -0.3333 -0.6667 0.0000
0.0000 0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
31
-0.6667 -0.3333 0.6667 0.0000
-0.3333 0.3333 1.3333 0.0000
0.6667 -0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
32
0.6667 -1.0000 0.6667 0.0000
0.3333 -1.0000 -0.6667 0.0000
-0.6667 0.0000 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
33
1.0000 -1.0000 -0.0000 0.0000
1.0000 0.0000 -0.0000 0.0000
0.0000 0.0000 -1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
34
-1.0000 0.3333 0.6667 0.0000
-1.0000 0.6667 -0.6667 0.0000
0.0000 0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
35
0.3333 -0.3333 -1.3333 0.0000
-0.3333 -0.6667 -0.6667 0.0000
0.6667 -0.6667 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
36
-0.3333 1.0000 0.6667 0.0000
0.3333 0.0000 1.3333 0.0000
-0.6667 0.0000 0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
37
1.0000 -0.3333 -0.6667 0.0000
0.0000 0.3333 -1.3333 0.0000
0.0000 -0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
38
-1.0000 1.0000 0.0000 0.0000
0.0000 1.0000 0.0000 0.0000
0.0000 0.0000 1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
39
0.3333 -1.0000 -0.6667 0.0000
0.6667 -1.0000 0.6667 0.0000
0.6667 0.0000 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
40
-0.3333 0.3333 1.3333 0.0000
-0.6667 -0.3333 0.6667 0.0000
-0.6667 0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
41
-0.3333 -0.6667 -0.6667 0.0000
0.3333 -0.3333 -1.3333 0.0000
-0.6667 0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
42
0.3333 0.0000 1.3333 0.0000
-0.3333 1.0000 0.6667 0.0000
0.6667 0.0000 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
43
1.0000 0.0000 0.0000 0.0000
1.0000 -1.0000 0.0000 0.0000
0.0000 0.0000 1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
44
-1.0000 0.6667 -0.6667 0.0000
-1.0000 0.3333 0.6667 0.0000
0.0000 -0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
45
-0.6667 1.0000 -0.6667 0.0000
-0.3333 0.0000 -1.3333 0.0000
0.6667 0.0000 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
46
0.6667 0.3333 -0.6667 0.0000
0.3333 0.6667 0.6667 0.0000
-0.6667 0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
47
0.0000 -0.3333 1.3333 0.0000
1.0000 -0.6667 0.6667 0.0000
0.0000 -0.6667 -0.3333 0.0000
0.0000 0.0000 0.0000 1.0000
48
0.0000 -1.0000 0.0000 0.0000
-1.0000 0.0000 0.0000 0.0000
0.0000 0.0000 1.0000 0.0000
0.0000 0.0000 0.0000 1.0000
49
1.0000 0.0000 0.0000 0.6667
0.0000 1.0000 0.0000 0.3333
0.0000 0.0000 1.0000 0.3333
0.0000 0.0000 0.0000 1.0000
50
-1.0000 0.6667 -0.6667 0.6667
0.0000 0.3333 -1.3333 0.3333
0.0000 -0.6667 -0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
51
-0.3333 -0.6667 -0.6667 0.6667
-0.6667 -0.3333 0.6667 0.3333
-0.6667 0.6667 -0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
52
0.3333 0.0000 1.3333 0.6667
0.6667 -1.0000 0.6667 0.3333
0.6667 0.0000 -0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
53
0.0000 -1.0000 0.0000 0.6667
1.0000 -1.0000 0.0000 0.3333
0.0000 0.0000 1.0000 0.3333
0.0000 0.0000 0.0000 1.0000
54
0.0000 -0.3333 1.3333 0.6667
-1.0000 0.3333 0.6667 0.3333
0.0000 -0.6667 -0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
55
0.6667 0.3333 -0.6667 0.6667
0.3333 -0.3333 -1.3333 0.3333
-0.6667 0.6667 -0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
56
-0.6667 1.0000 -0.6667 0.6667
-0.3333 1.0000 0.6667 0.3333
0.6667 0.0000 -0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
57
-1.0000 1.0000 0.0000 0.6667
-1.0000 0.0000 0.0000 0.3333
0.0000 0.0000 1.0000 0.3333
0.0000 0.0000 0.0000 1.0000
58
1.0000 -0.3333 -0.6667 0.6667
1.0000 -0.6667 0.6667 0.3333
0.0000 -0.6667 -0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
59
-0.3333 0.3333 1.3333 0.6667
0.3333 0.6667 0.6667 0.3333
-0.6667 0.6667 -0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
60
0.3333 -1.0000 -0.6667 0.6667
-0.3333 0.0000 -1.3333 0.3333
0.6667 0.0000 -0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
61
-1.0000 0.3333 0.6667 0.6667
0.0000 -0.3333 1.3333 0.3333
0.0000 0.6667 0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
62
1.0000 -1.0000 -0.0000 0.6667
0.0000 -1.0000 -0.0000 0.3333
0.0000 0.0000 -1.0000 0.3333
0.0000 0.0000 0.0000 1.0000
63
-0.3333 1.0000 0.6667 0.6667
-0.6667 1.0000 -0.6667 0.3333
-0.6667 0.0000 0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
64
0.3333 -0.3333 -1.3333 0.6667
0.6667 0.3333 -0.6667 0.3333
0.6667 -0.6667 0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
65
0.3333 0.6667 0.6667 0.6667
-0.3333 0.3333 1.3333 0.3333
0.6667 -0.6667 0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
66
-0.3333 0.0000 -1.3333 0.6667
0.3333 -1.0000 -0.6667 0.3333
-0.6667 0.0000 0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
67
-1.0000 0.0000 -0.0000 0.6667
-1.0000 1.0000 -0.0000 0.3333
0.0000 0.0000 -1.0000 0.3333
0.0000 0.0000 0.0000 1.0000
68
1.0000 -0.6667 0.6667 0.6667
1.0000 -0.3333 -0.6667 0.3333
0.0000 0.6667 0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
69
0.6667 -1.0000 0.6667 0.6667
0.3333 0.0000 1.3333 0.3333
-0.6667 0.0000 0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
70
-0.6667 -0.3333 0.6667 0.6667
-0.3333 -0.6667 -0.6667 0.3333
0.6667 -0.6667 0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
71
0.0000 0.3333 -1.3333 0.6667
-1.0000 0.6667 -0.6667 0.3333
0.0000 0.6667 0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
72
0.0000 1.0000 -0.0000 0.6667
1.0000 0.0000 -0.0000 0.3333
0.0000 0.0000 -1.0000 0.3333
0.0000 0.0000 0.0000 1.0000
73
-1.0000 0.0000 -0.0000 0.6667
0.0000 -1.0000 -0.0000 0.3333
0.0000 0.0000 -1.0000 0.3333
0.0000 0.0000 0.0000 1.0000
74
1.0000 -0.6667 0.6667 0.6667
0.0000 -0.3333 1.3333 0.3333
0.0000 0.6667 0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
75
0.3333 0.6667 0.6667 0.6667
0.6667 0.3333 -0.6667 0.3333
0.6667 -0.6667 0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
76
-0.3333 0.0000 -1.3333 0.6667
-0.6667 1.0000 -0.6667 0.3333
-0.6667 0.0000 0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
77
0.0000 1.0000 -0.0000 0.6667
-1.0000 1.0000 -0.0000 0.3333
0.0000 0.0000 -1.0000 0.3333
0.0000 0.0000 0.0000 1.0000
78
0.0000 0.3333 -1.3333 0.6667
1.0000 -0.3333 -0.6667 0.3333
0.0000 0.6667 0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
79
-0.6667 -0.3333 0.6667 0.6667
-0.3333 0.3333 1.3333 0.3333
0.6667 -0.6667 0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
80
0.6667 -1.0000 0.6667 0.6667
0.3333 -1.0000 -0.6667 0.3333
-0.6667 0.0000 0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
81
1.0000 -1.0000 -0.0000 0.6667
1.0000 0.0000 -0.0000 0.3333
0.0000 0.0000 -1.0000 0.3333
0.0000 0.0000 0.0000 1.0000
82
-1.0000 0.3333 0.6667 0.6667
-1.0000 0.6667 -0.6667 0.3333
0.0000 0.6667 0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
83
0.3333 -0.3333 -1.3333 0.6667
-0.3333 -0.6667 -0.6667 0.3333
0.6667 -0.6667 0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
84
-0.3333 1.0000 0.6667 0.6667
0.3333 0.0000 1.3333 0.3333
-0.6667 0.0000 0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
85
1.0000 -0.3333 -0.6667 0.6667
0.0000 0.3333 -1.3333 0.3333
0.0000 -0.6667 -0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
86
-1.0000 1.0000 0.0000 0.6667
0.0000 1.0000 0.0000 0.3333
0.0000 0.0000 1.0000 0.3333
0.0000 0.0000 0.0000 1.0000
87
0.3333 -1.0000 -0.6667 0.6667
0.6667 -1.0000 0.6667 0.3333
0.6667 0.0000 -0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
88
-0.3333 0.3333 1.3333 0.6667
-0.6667 -0.3333 0.6667 0.3333
-0.6667 0.6667 -0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
89
-0.3333 -0.6667 -0.6667 0.6667
0.3333 -0.3333 -1.3333 0.3333
-0.6667 0.6667 -0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
90
0.3333 0.0000 1.3333 0.6667
-0.3333 1.0000 0.6667 0.3333
0.6667 0.0000 -0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
91
1.0000 0.0000 0.0000 0.6667
1.0000 -1.0000 0.0000 0.3333
0.0000 0.0000 1.0000 0.3333
0.0000 0.0000 0.0000 1.0000
92
-1.0000 0.6667 -0.6667 0.6667
-1.0000 0.3333 0.6667 0.3333
0.0000 -0.6667 -0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
93
-0.6667 1.0000 -0.6667 0.6667
-0.3333 0.0000 -1.3333 0.3333
0.6667 0.0000 -0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
94
0.6667 0.3333 -0.6667 0.6667
0.3333 0.6667 0.6667 0.3333
-0.6667 0.6667 -0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
95
0.0000 -0.3333 1.3333 0.6667
1.0000 -0.6667 0.6667 0.3333
0.0000 -0.6667 -0.3333 0.3333
0.0000 0.0000 0.0000 1.0000
96
0.0000 -1.0000 0.0000 0.6667
-1.0000 0.0000 0.0000 0.3333
0.0000 0.0000 1.0000 0.3333
0.0000 0.0000 0.0000 1.0000
97
1.0000 0.0000 0.0000 0.3333
0.0000 1.0000 0.0000 0.6667
0.0000 0.0000 1.0000 0.6667
0.0000 0.0000 0.0000 1.0000
98
-1.0000 0.6667 -0.6667 0.3333
0.0000 0.3333 -1.3333 0.6667
0.0000 -0.6667 -0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
99
-0.3333 -0.6667 -0.6667 0.3333
-0.6667 -0.3333 0.6667 0.6667
-0.6667 0.6667 -0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
100
0.3333 0.0000 1.3333 0.3333
0.6667 -1.0000 0.6667 0.6667
0.6667 0.0000 -0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
101
0.0000 -1.0000 0.0000 0.3333
1.0000 -1.0000 0.0000 0.6667
0.0000 0.0000 1.0000 0.6667
0.0000 0.0000 0.0000 1.0000
102
0.0000 -0.3333 1.3333 0.3333
-1.0000 0.3333 0.6667 0.6667
0.0000 -0.6667 -0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
103
0.6667 0.3333 -0.6667 0.3333
0.3333 -0.3333 -1.3333 0.6667
-0.6667 0.6667 -0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
104
-0.6667 1.0000 -0.6667 0.3333
-0.3333 1.0000 0.6667 0.6667
0.6667 0.0000 -0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
105
-1.0000 1.0000 0.0000 0.3333
-1.0000 0.0000 0.0000 0.6667
0.0000 0.0000 1.0000 0.6667
0.0000 0.0000 0.0000 1.0000
106
1.0000 -0.3333 -0.6667 0.3333
1.0000 -0.6667 0.6667 0.6667
0.0000 -0.6667 -0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
107
-0.3333 0.3333 1.3333 0.3333
0.3333 0.6667 0.6667 0.6667
-0.6667 0.6667 -0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
108
0.3333 -1.0000 -0.6667 0.3333
-0.3333 0.0000 -1.3333 0.6667
0.6667 0.0000 -0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
109
-1.0000 0.3333 0.6667 0.3333
0.0000 -0.3333 1.3333 0.6667
0.0000 0.6667 0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
110
1.0000 -1.0000 -0.0000 0.3333
0.0000 -1.0000 -0.0000 0.6667
0.0000 0.0000 -1.0000 0.6667
0.0000 0.0000 0.0000 1.0000
111
-0.3333 1.0000 0.6667 0.3333
-0.6667 1.0000 -0.6667 0.6667
-0.6667 0.0000 0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
112
0.3333 -0.3333 -1.3333 0.3333
0.6667 0.3333 -0.6667 0.6667
0.6667 -0.6667 0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
113
0.3333 0.6667 0.6667 0.3333
-0.3333 0.3333 1.3333 0.6667
0.6667 -0.6667 0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
114
-0.3333 0.0000 -1.3333 0.3333
0.3333 -1.0000 -0.6667 0.6667
-0.6667 0.0000 0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
115
-1.0000 0.0000 -0.0000 0.3333
-1.0000 1.0000 -0.0000 0.6667
0.0000 0.0000 -1.0000 0.6667
0.0000 0.0000 0.0000 1.0000
116
1.0000 -0.6667 0.6667 0.3333
1.0000 -0.3333 -0.6667 0.6667
0.0000 0.6667 0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
117
0.6667 -1.0000 0.6667 0.3333
0.3333 0.0000 1.3333 0.6667
-0.6667 0.0000 0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
118
-0.6667 -0.3333 0.6667 0.3333
-0.3333 -0.6667 -0.6667 0.6667
0.6667 -0.6667 0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
119
0.0000 0.3333 -1.3333 0.3333
-1.0000 0.6667 -0.6667 0.6667
0.0000 0.6667 0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
120
0.0000 1.0000 -0.0000 0.3333
1.0000 0.0000 -0.0000 0.6667
0.0000 0.0000 -1.0000 0.6667
0.0000 0.0000 0.0000 1.0000
121
-1.0000 0.0000 -0.0000 0.3333
0.0000 -1.0000 -0.0000 0.6667
0.0000 0.0000 -1.0000 0.6667
0.0000 0.0000 0.0000 1.0000
122
1.0000 -0.6667 0.6667 0.3333
0.0000 -0.3333 1.3333 0.6667
0.0000 0.6667 0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
123
0.3333 0.6667 0.6667 0.3333
0.6667 0.3333 -0.6667 0.6667
0.6667 -0.6667 0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
124
-0.3333 0.0000 -1.3333 0.3333
-0.6667 1.0000 -0.6667 0.6667
-0.6667 0.0000 0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
125
0.0000 1.0000 -0.0000 0.3333
-1.0000 1.0000 -0.0000 0.6667
0.0000 0.0000 -1.0000 0.6667
0.0000 0.0000 0.0000 1.0000
126
0.0000 0.3333 -1.3333 0.3333
1.0000 -0.3333 -0.6667 0.6667
0.0000 0.6667 0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
127
-0.6667 -0.3333 0.6667 0.3333
-0.3333 0.3333 1.3333 0.6667
0.6667 -0.6667 0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
128
0.6667 -1.0000 0.6667 0.3333
0.3333 -1.0000 -0.6667 0.6667
-0.6667 0.0000 0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
129
1.0000 -1.0000 -0.0000 0.3333
1.0000 0.0000 -0.0000 0.6667
0.0000 0.0000 -1.0000 0.6667
0.0000 0.0000 0.0000 1.0000
130
-1.0000 0.3333 0.6667 0.3333
-1.0000 0.6667 -0.6667 0.6667
0.0000 0.6667 0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
131
0.3333 -0.3333 -1.3333 0.3333
-0.3333 -0.6667 -0.6667 0.6667
0.6667 -0.6667 0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
132
-0.3333 1.0000 0.6667 0.3333
0.3333 0.0000 1.3333 0.6667
-0.6667 0.0000 0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
133
1.0000 -0.3333 -0.6667 0.3333
0.0000 0.3333 -1.3333 0.6667
0.0000 -0.6667 -0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
134
-1.0000 1.0000 0.0000 0.3333
0.0000 1.0000 0.0000 0.6667
0.0000 0.0000 1.0000 0.6667
0.0000 0.0000 0.0000 1.0000
135
0.3333 -1.0000 -0.6667 0.3333
0.6667 -1.0000 0.6667 0.6667
0.6667 0.0000 -0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
136
-0.3333 0.3333 1.3333 0.3333
-0.6667 -0.3333 0.6667 0.6667
-0.6667 0.6667 -0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
137
-0.3333 -0.6667 -0.6667 0.3333
0.3333 -0.3333 -1.3333 0.6667
-0.6667 0.6667 -0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
138
0.3333 0.0000 1.3333 0.3333
-0.3333 1.0000 0.6667 0.6667
0.6667 0.0000 -0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
139
1.0000 0.0000 0.0000 0.3333
1.0000 -1.0000 0.0000 0.6667
0.0000 0.0000 1.0000 0.6667
0.0000 0.0000 0.0000 1.0000
140
-1.0000 0.6667 -0.6667 0.3333
-1.0000 0.3333 0.6667 0.6667
0.0000 -0.6667 -0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
141
-0.6667 1.0000 -0.6667 0.3333
-0.3333 0.0000 -1.3333 0.6667
0.6667 0.0000 -0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
142
0.6667 0.3333 -0.6667 0.3333
0.3333 0.6667 0.6667 0.6667
-0.6667 0.6667 -0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
143
0.0000 -0.3333 1.3333 0.3333
1.0000 -0.6667 0.6667 0.6667
0.0000 -0.6667 -0.3333 0.6667
0.0000 0.0000 0.0000 1.0000
144
0.0000 -1.0000 0.0000 0.3333
-1.0000 0.0000 0.0000 0.6667
0.0000 0.0000 1.0000 0.6667
0.0000 0.0000 0.0000 1.0000
To summarize: we had 48 symmetry operators in our high symmetry space group Pm3m (#221), then under the applied transformation, the unit cell expanded 3 times of its initial value, with some of the previously symmetry operations connected via lattice translations now acting in the same unit cell to a total of \(48x3=144\). However, now that we are interested in a lower symmetry space group’s (R3m (#166)) settings, some of the symmetry elements has been lost due to the symmetry break accompanying the transition and of the 144 transformed operators, we ended with only 36 being active.
Wyckoff Positions Splitting¶
The loss of some of the symmetry elements manifests itself such that previously connected sites in the high symmetry structure can no longer be related in the low symmetry structure because they are no longer assumed to be equivalent. This can be due to a couple of factors, some of them being:
Changes in their positions:
Consider the two sites \(A(0.5,0,0)\) and \(B(0,0.5,0)\) connected by the 4-fold rotation operator \(4\) in the high symmetry structure. However, imagine that, under an applied strain along the \(a\) direction, the atom at site A moves to \(A'(0.51,0,0)\) and the two atoms can no longer be connected via the \(4\) operator, thus the \(4\) symmetry is lost and the resulting structure under the strain now belongs to a lower symmetry.Changes in the species:
In this scenario, imagine that there are two sites \(A(0.5,0,0)\) and \(B(0,0.5,0)\) with F atoms occupying them. They are connected by the 4-fold rotation operator. However, let’s assume that, by means of chemical process, the F atom at site \(A\) is removed and a Cl atom is substituted in its place. In this situation, even though the site positions haven’t changed, the equivalency (hence the symmetry) is broken due to the different species occupying the sites.Difference in magnetic moments:
Even the two Ti atoms’ site positions \(A(0.5,0,0)\) and \(B(0,0.5,0)\) are related through the \(4\) operator, and even though they are of the same species, their magnetic moments can have different orientations. (The inclusion and treatment of magnetic properties lead to the magnetic space groups which we won’t delve into)
Take the position \(X(0.1,0.1,0.1)\) in the Pm3m (#221) space group. In this group’s setting, let’s calculate its multiplicity and the elements of the orbit it belongs to:
import re
orbit_221 = []
site = np.array([[0.1],[0.1],[0.1],[1]])
print("Calculating the orbit of:\n X({:5.2f},{:5.2f},{:5.2f})"\
.format(*site.flatten()))
for i in range(len(ops)):
operator = ops[i]
op_site = np.dot(operator, site)
label = re.sub(r'(.*)[ ]+\|\|.*$',r'\1',labels[i])
label = label.strip()
label = re.sub(r'[ ]+',' ',label)
print("{:2d}. [{:^12s}].X: ({:5.2f},{:5.2f},{:5.2f})"\
.format(i+1,label,*op_site.flatten()),end="")
if(np.any(op_site<0) or np.any(op_site>=1)):
op_site = op_site - np.floor(op_site)
print(" -> ({:.2f},{:.2f},{:.2f})"\
.format(*op_site.flatten()),end="")
orbit_221.append(op_site)
print("")
# Remove the duplicate sites in the orbit
orbit_221 = np.unique(orbit_221,axis=0)
print("-"*30)
Calculating the orbit of:
X( 0.10, 0.10, 0.10)
1. [ 1 ].X: ( 0.10, 0.10, 0.10) -> (0.10,0.10,0.10)
2. [ 2 0,0,z ].X: (-0.10,-0.10, 0.10) -> (0.90,0.90,0.10)
3. [ 2 0,y,0 ].X: (-0.10, 0.10,-0.10) -> (0.90,0.10,0.90)
4. [ 2 x,0,0 ].X: ( 0.10,-0.10,-0.10) -> (0.10,0.90,0.90)
5. [ 3- x,x,x ].X: ( 0.10, 0.10, 0.10) -> (0.10,0.10,0.10)
6. [ 3- -x,x,-x ].X: ( 0.10,-0.10,-0.10) -> (0.10,0.90,0.90)
7. [ 3- x,-x,-x ].X: (-0.10,-0.10, 0.10) -> (0.90,0.90,0.10)
8. [ 3- -x,-x,x ].X: (-0.10, 0.10,-0.10) -> (0.90,0.10,0.90)
9. [ 3+ x,x,x ].X: ( 0.10, 0.10, 0.10) -> (0.10,0.10,0.10)
10. [ 3+ x,-x,-x ].X: (-0.10, 0.10,-0.10) -> (0.90,0.10,0.90)
11. [ 3+ -x,-x,x ].X: ( 0.10,-0.10,-0.10) -> (0.10,0.90,0.90)
12. [ 3+ -x,x,-x ].X: (-0.10,-0.10, 0.10) -> (0.90,0.90,0.10)
13. [ 2 x,x,0 ].X: ( 0.10, 0.10,-0.10) -> (0.10,0.10,0.90)
14. [ 2 x,-x,0 ].X: (-0.10,-0.10,-0.10) -> (0.90,0.90,0.90)
15. [ 4+ 0,0,z ].X: ( 0.10,-0.10, 0.10) -> (0.10,0.90,0.10)
16. [ 4- 0,0,z ].X: (-0.10, 0.10, 0.10) -> (0.90,0.10,0.10)
17. [ 4+ x,0,0 ].X: ( 0.10, 0.10,-0.10) -> (0.10,0.10,0.90)
18. [ 2 0,y,y ].X: (-0.10, 0.10, 0.10) -> (0.90,0.10,0.10)
19. [ 2 0,y,-y ].X: (-0.10,-0.10,-0.10) -> (0.90,0.90,0.90)
20. [ 4- x,0,0 ].X: ( 0.10,-0.10, 0.10) -> (0.10,0.90,0.10)
21. [ 4- 0,y,0 ].X: ( 0.10, 0.10,-0.10) -> (0.10,0.10,0.90)
22. [ 2 x,0,x ].X: ( 0.10,-0.10, 0.10) -> (0.10,0.90,0.10)
23. [ 4+ 0,y,0 ].X: (-0.10, 0.10, 0.10) -> (0.90,0.10,0.10)
24. [ 2 -x,0,x ].X: (-0.10,-0.10,-0.10) -> (0.90,0.90,0.90)
25. [ -1 0,0,0 ].X: (-0.10,-0.10,-0.10) -> (0.90,0.90,0.90)
26. [ m x,y,0 ].X: ( 0.10, 0.10,-0.10) -> (0.10,0.10,0.90)
27. [ m x,0,z ].X: ( 0.10,-0.10, 0.10) -> (0.10,0.90,0.10)
28. [ m 0,y,z ].X: (-0.10, 0.10, 0.10) -> (0.90,0.10,0.10)
29. [-3- x,x,x; 0,0,0].X: (-0.10,-0.10,-0.10) -> (0.90,0.90,0.90)
30. [-3- -x,x,-x; 0,0,0].X: (-0.10, 0.10, 0.10) -> (0.90,0.10,0.10)
31. [-3- x,-x,-x; 0,0,0].X: ( 0.10, 0.10,-0.10) -> (0.10,0.10,0.90)
32. [-3- -x,-x,x; 0,0,0].X: ( 0.10,-0.10, 0.10) -> (0.10,0.90,0.10)
33. [-3+ x,x,x; 0,0,0].X: (-0.10,-0.10,-0.10) -> (0.90,0.90,0.90)
34. [-3+ x,-x,-x; 0,0,0].X: ( 0.10,-0.10, 0.10) -> (0.10,0.90,0.10)
35. [-3+ -x,-x,x; 0,0,0].X: (-0.10, 0.10, 0.10) -> (0.90,0.10,0.10)
36. [-3+ -x,x,-x; 0,0,0].X: ( 0.10, 0.10,-0.10) -> (0.10,0.10,0.90)
37. [ m x,-x,z ].X: (-0.10,-0.10, 0.10) -> (0.90,0.90,0.10)
38. [ m x,x,z ].X: ( 0.10, 0.10, 0.10) -> (0.10,0.10,0.10)
39. [-4+ 0,0,z; 0,0,0].X: (-0.10, 0.10,-0.10) -> (0.90,0.10,0.90)
40. [-4- 0,0,z; 0,0,0].X: ( 0.10,-0.10,-0.10) -> (0.10,0.90,0.90)
41. [-4+ x,0,0; 0,0,0].X: (-0.10,-0.10, 0.10) -> (0.90,0.90,0.10)
42. [ m x,y,-y ].X: ( 0.10,-0.10,-0.10) -> (0.10,0.90,0.90)
43. [ m x,y,y ].X: ( 0.10, 0.10, 0.10) -> (0.10,0.10,0.10)
44. [-4- x,0,0; 0,0,0].X: (-0.10, 0.10,-0.10) -> (0.90,0.10,0.90)
45. [-4- 0,y,0; 0,0,0].X: (-0.10,-0.10, 0.10) -> (0.90,0.90,0.10)
46. [ m -x,y,x ].X: (-0.10, 0.10,-0.10) -> (0.90,0.10,0.90)
47. [-4+ 0,y,0; 0,0,0].X: ( 0.10,-0.10,-0.10) -> (0.10,0.90,0.90)
48. [ m x,y,x ].X: ( 0.10, 0.10, 0.10) -> (0.10,0.10,0.10)
------------------------------
print("After taking out the duplicates, the orbit is as follows:")
for i,orb_element in enumerate(orbit_221,start=1):
print("{:2d}. ({:.2f},{:.2f},{:.2f})"\
.format(i,*orb_element.flatten()))
print("Hence, the multiplicity of this Wyckoff position is: {:d}"\
.format(i))
After taking out the duplicates, the orbit is as follows:
1. (0.10,0.10,0.10)
2. (0.10,0.10,0.90)
3. (0.10,0.90,0.10)
4. (0.10,0.90,0.90)
5. (0.90,0.10,0.10)
6. (0.90,0.10,0.90)
7. (0.90,0.90,0.10)
8. (0.90,0.90,0.90)
Hence, the multiplicity of this Wyckoff position is: 8
The \((x,x,x)\) site in Pm3m (#221) is actually: 8g as can be checked against the Wyckoff Positions listing in Structure chapter’s corresponding table. Here it is visualized in all its glory:
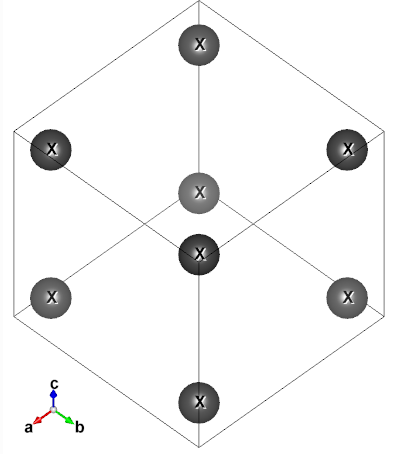
So, with the unit cell volume tripled under the transformation, the number of atomic sites will also triple, e.g., if there were 1 Ba atom in the previous unit cell, not there will be 1x3=3 Ba atoms in the new unit cell; the 3 O atoms in the previous unit cell will be 3x3=9 O atoms in the new unit cell; similarly if we had 8 X atoms in the 8g Wyckoff position, they will now span 8x2=24 atomic sites in the unit cell. So far, so good! 8)
Let’s find those 24 sites: We will first use the transformed operators of Pm3m (#221) and then re-do the calculations using the 36 operators of R3m (#166)
# #221 -> #166 [4]
P = np.array([[1,0,1,0],\
[-1,1,1,0],\
[0,-1,1,0],\
[0,0,0,1]])
P_inv = np.linalg.inv(P)
X = np.array([[0.1],[0.1],[0.1],[1]])
X_p = np.dot(P_inv,X)
print("Position in group basis: ",("{:6.4f} "*3).format((*X.flatten()[:3])))
print("="*46)
print("Position in subgroup basis:")
positions_in_166 = []
for t_x in range(2):
for t_y in range(2):
for t_z in range(2):
a = X_p + np.array([[t_x],[t_y],[t_z],[0]])
for op in ops:
op = np.linalg.multi_dot((P_inv,op,P))
ap = np.dot(op,X)
ap -= np.floor(ap)
ap[np.abs(ap)<1E-15] = 0
flag_not_found = True
for i in positions_in_166:
if(np.allclose(ap,i)):
flag_not_found = False
break
if(flag_not_found):
positions_in_166.append(ap)
for (i,orb_element) in enumerate(positions_in_166,start=1):
print(("{:2d}"+"{:8.4f} "*3).format(i,*orb_element.flatten()))
print("[Table A]")
Position in group basis: 0.1000 0.1000 0.1000
==============================================
Position in subgroup basis:
1 0.1000 0.1000 0.1000
2 0.9000 0.9000 0.9000
3 0.8333 0.9667 0.9667
4 0.1667 0.0333 0.0333
5 0.9000 0.0000 0.1000
6 0.1000 1.0000 0.9000
7 0.0333 0.8667 0.9667
8 0.9667 0.1333 0.0333
9 0.0000 0.9000 0.1000
10 1.0000 0.1000 0.9000
11 0.1333 0.1667 0.9667
12 0.8667 0.8333 0.0333
13 0.0000 0.1000 0.1000
14 1.0000 0.9000 0.9000
15 0.1333 0.9667 0.9667
16 0.8667 0.0333 0.0333
17 0.1667 0.1333 0.0333
18 0.8333 0.8667 0.9667
19 0.9000 1.0000 0.9000
20 0.1000 0.0000 0.1000
21 0.0333 0.1667 0.9667
22 0.9667 0.8333 0.0333
23 0.9000 0.9000 0.1000
24 0.1000 0.1000 0.9000
[Table A]
Symmetry operators of R3m (#166) in matrix representation is as follows:
ops_166=[]
labels_166=[]
ops_166.append(np.array([[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
labels_166.append("1 || x,y,z")
ops_166.append(np.array([[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[1.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
labels_166.append("3- 0,0,z || -y,x-y,z")
ops_166.append(np.array([[-1.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
labels_166.append("3+ 0,0,z || -x+y,-x,z")
ops_166.append(np.array([[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
labels_166.append("2 x,x,0 || y,x,-z")
ops_166.append(np.array([[1.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
labels_166.append("2 2x,-x,0 || x-y,-y,-z")
ops_166.append(np.array([[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[-1.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
labels_166.append("2 x,-2x,0 || -x,-x+y,-z")
ops_166.append(np.array([[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
labels_166.append("-1 0,0,0 || -x,-y,-z")
ops_166.append(np.array([[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[-1.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
labels_166.append("-3- 0,0,z; 0,0,0 || y,-x+y,-z")
ops_166.append(np.array([[1.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
labels_166.append("-3+ 0,0,z; 0,0,0 || x-y,x,-z")
ops_166.append(np.array([[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
labels_166.append("m x,-x,z || -y,-x,z")
ops_166.append(np.array([[-1.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
labels_166.append("m 4x,5x,z || -x+y,y,z")
ops_166.append(np.array([[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[1.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,0.000000000000E+00],[0,0,0,1.000000000000E+00]]))
labels_166.append("m 5x,4x,z || x,x-y,z")
ops_166.append(np.array([[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,3.333333333333E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("t (2/3,1/3,1/3) || x+2/3,y+1/3,z+1/3")
ops_166.append(np.array([[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[1.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,3.333333333333E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("3- (0,0,1/3) 5/9,-1/9,z || -y+2/3,x-y+1/3,z+1/3")
ops_166.append(np.array([[-1.000000000000E+00,1.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,3.333333333333E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("3+ (0,0,1/3) 1/9,4/9,z || -x+y+2/3,-x+1/3,z+1/3")
ops_166.append(np.array([[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,3.333333333333E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("2 (1/2,1/2,0) x,x-1/6,1/6 || y+2/3,x+1/3,-z+1/3")
ops_166.append(np.array([[1.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,3.333333333333E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("2 (2/3,-1/3,0) 2x,-x+1/3,1/6 || x-y+2/3,-y+1/3,-z+1/3")
ops_166.append(np.array([[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[-1.000000000000E+00,1.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,3.333333333333E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("2 (-1/6,1/3,0) x,-2x+5/6,1/6 || -x+2/3,-x+y+1/3,-z+1/3")
ops_166.append(np.array([[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,3.333333333333E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("-1 1/3,1/6,1/6 || -x+2/3,-y+1/3,-z+1/3")
ops_166.append(np.array([[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[-1.000000000000E+00,1.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,3.333333333333E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("-3- -1/3,1,z; -1/3,1,1/6 || y+2/3,-x+y+1/3,-z+1/3")
ops_166.append(np.array([[1.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,3.333333333333E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("-3+ 1,-2/3,z; 1,-2/3,1/6 || x-y+2/3,x+1/3,-z+1/3")
ops_166.append(np.array([[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,3.333333333333E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("g (1/6,-1/6,1/3) x+1/2,-x,z || -y+2/3,-x+1/3,z+1/3")
ops_166.append(np.array([[-1.000000000000E+00,1.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,3.333333333333E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("g (0,2/3,1/3) 4x+0.46667,5x,z || -x+y+2/3,y+1/3,z+1/3")
ops_166.append(np.array([[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[1.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,3.333333333333E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("g (5/6,0,1/3) 5x-0.29167,4x,z || x+2/3,x-y+1/3,z+1/3")
ops_166.append(np.array([[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,6.666666666667E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("t (1/3,2/3,2/3) || x+1/3,y+2/3,z+2/3")
ops_166.append(np.array([[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[1.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,6.666666666667E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("3- (0,0,2/3) 4/9,1/9,z || -y+1/3,x-y+2/3,z+2/3")
ops_166.append(np.array([[-1.000000000000E+00,1.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,6.666666666667E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("3+ (0,0,2/3) -1/9,5/9,z || -x+y+1/3,-x+2/3,z+2/3")
ops_166.append(np.array([[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,6.666666666667E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("2 (1/2,1/2,0) x,x+1/6,1/3 || y+1/3,x+2/3,-z+2/3")
ops_166.append(np.array([[1.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,6.666666666667E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("2 (1/3,-1/6,0) 2x,-x+5/12,1/3 || x-y+1/3,-y+2/3,-z+2/3")
ops_166.append(np.array([[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[-1.000000000000E+00,1.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,6.666666666667E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("2 (-1/3,2/3,0) x,-2x+2/3,1/3 || -x+1/3,-x+y+2/3,-z+2/3")
ops_166.append(np.array([[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,6.666666666667E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("-1 1/6,1/3,1/3 || -x+1/3,-y+2/3,-z+2/3")
ops_166.append(np.array([[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[-1.000000000000E+00,1.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,6.666666666667E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("-3- -2/3,1,z; -2/3,1,1/3 || y+1/3,-x+y+2/3,-z+2/3")
ops_166.append(np.array([[1.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[0.000000000000E+00,0.000000000000E+00,-1.000000000000E+00,6.666666666667E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("-3+ 1,-1/3,z; 1,-1/3,1/3 || x-y+1/3,x+2/3,-z+2/3")
ops_166.append(np.array([[0.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[-1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,6.666666666667E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("g (-1/6,1/6,2/3) x+1/2,-x,z || -y+1/3,-x+2/3,z+2/3")
ops_166.append(np.array([[-1.000000000000E+00,1.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[0.000000000000E+00,1.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,6.666666666667E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("g (0,5/6,2/3) 4x+0.23333,5x,z || -x+y+1/3,y+2/3,z+2/3")
ops_166.append(np.array([[1.000000000000E+00,0.000000000000E+00,0.000000000000E+00,3.333333333333E-01],[1.000000000000E+00,-1.000000000000E+00,0.000000000000E+00,6.666666666667E-01],[0.000000000000E+00,0.000000000000E+00,1.000000000000E+00,6.666666666667E-01],[0,0,0,1.000000000000E+00]]))
labels_166.append("g (2/3,0,2/3) 5x-7/12,4x,z || x+1/3,x-y+2/3,z+2/3")
We first transform our point \(X(0.1,0.1,0.1)\) coordinates in Pm3m (#221) to the settings of R3m (#166) via the position transformation formula:
Then, we will apply the 36 symmetry operations to this point to derive its corresponding orbit in the subgroup (spoiler alert: we expect it to be of multiplicity 3x8=24 but it won’t be! ;)
X = np.array([[0.1],[0.1],[0.1],[1]])
X_p = np.dot(P_inv,X)
print(" Position in group basis: ",("{:6.4f} "*3)\
.format((*X.flatten()[:3])))
print("Corresponding position in subgroup basis: ",("{:6.4f} "*3)\
.format((*X_p.flatten()[:3])))
print("="*63)
print("Position in subgroup basis:")
positions_166_w_36op_x_rep = []
for t_x in range(2):
for t_y in range(2):
for t_z in range(2):
a = X_p + np.array([[t_x],[t_y],[t_z],[0]])
for op in ops_166:
ap = np.dot(op,a)
ap -= np.floor(ap)
ap[np.isclose(ap,np.array([1,1,1,0]).reshape(4,1))]= 0
ap[np.abs(ap)<1E-15] = 0
flag_not_found = True
for i in positions_166_w_36op_x_rep:
if(np.allclose(ap,i)):
flag_not_found = False
break
if(flag_not_found):
positions_166_w_36op_x_rep.append(ap)
for (i,wp) in enumerate(positions_166_w_36op_x_rep,start=1):
print(("{:2d}"+"{:8.4f} "*3).format(i,*wp.flatten()))
print("[Table B]")
Position in group basis: 0.1000 0.1000 0.1000
Corresponding position in subgroup basis: 0.0000 0.0000 0.1000
===============================================================
Position in subgroup basis:
1 0.0000 0.0000 0.1000
2 0.0000 0.0000 0.9000
3 0.6667 0.3333 0.4333
4 0.6667 0.3333 0.2333
5 0.3333 0.6667 0.7667
6 0.3333 0.6667 0.5667
[Table B]
We were expecting 24 positions but ended up with 6 – where are the remaining 18? To find them, we are going to transform the orbit of our \(X\) position in Pm3m (#221) to the settings of R3m (#166). So, let’s use that orbit:
print("The orbit of X(0.1,0.1,0.1) in Pm-3m (#221):")
print("="*46)
for i,orb_element in enumerate(orbit_221,start=1):
print(("{:2d}. "+("{:6.4f} "*3))\
.format(i,(*orb_element.flatten()[:3])))
The orbit of X(0.1,0.1,0.1) in Pm-3m (#221):
==============================================
1. 0.1000 0.1000 0.1000
2. 0.1000 0.1000 0.9000
3. 0.1000 0.9000 0.1000
4. 0.1000 0.9000 0.9000
5. 0.9000 0.1000 0.1000
6. 0.9000 0.1000 0.9000
7. 0.9000 0.9000 0.1000
8. 0.9000 0.9000 0.9000
And here we are, transforming each of the orbit element to the R3m (#166) setting:
import re
orbit_166 = []
P = np.array([[1,0,1,0],\
[-1,1,1,0],\
[0,-1,1,0],\
[0,0,0,1]])
P_inv = np.linalg.inv(P)
for i,X in enumerate(orbit_221,start=1):
X_p = np.dot(P_inv,X)
X_p[:3] -= np.floor(X_p[:3])
print("{:2d}. X({:5.2f},{:5.2f},{:5.2f})@#221 -> X'({:5.2f},{:5.2f},{:5.2f})@#166"\
.format(i,*X.flatten()[:3],*X_p.flatten()))
orbit_166.append(X_p)
# Remove the duplicate sites in the orbit
orbit_166 = np.unique(orbit_166,axis=0)
print("-"*30)
print("After taking out the duplicates, the orbit is as follows:")
for i,orb_element in enumerate(orbit_166,start=1):
print("{:2d}. ({:.2f},{:.2f},{:.2f})"\
.format(i,*orb_element.flatten()))
print ("[Table C]")
print("\nHence, the multiplicity of this Wyckoff position is: {:d}"\
.format(i))
1. X( 0.10, 0.10, 0.10)@#221 -> X'( 0.00, 0.00, 0.10)@#166
2. X( 0.10, 0.10, 0.90)@#221 -> X'( 0.73, 0.47, 0.37)@#166
3. X( 0.10, 0.90, 0.10)@#221 -> X'( 0.73, 0.27, 0.37)@#166
4. X( 0.10, 0.90, 0.90)@#221 -> X'( 0.47, 0.73, 0.63)@#166
5. X( 0.90, 0.10, 0.10)@#221 -> X'( 0.53, 0.27, 0.37)@#166
6. X( 0.90, 0.10, 0.90)@#221 -> X'( 0.27, 0.73, 0.63)@#166
7. X( 0.90, 0.90, 0.10)@#221 -> X'( 0.27, 0.53, 0.63)@#166
8. X( 0.90, 0.90, 0.90)@#221 -> X'( 0.00, 0.00, 0.90)@#166
------------------------------
After taking out the duplicates, the orbit is as follows:
1. (0.00,0.00,0.10)
2. (0.00,0.00,0.90)
3. (0.27,0.53,0.63)
4. (0.27,0.73,0.63)
5. (0.47,0.73,0.63)
6. (0.53,0.27,0.37)
7. (0.73,0.27,0.37)
8. (0.73,0.47,0.37)
[Table C]
Hence, the multiplicity of this Wyckoff position is: 8
The first two entries \((0,0,0.10)\) and \((0,0,0.9)\) of the Table B are already among the among the found ones, and by starting from one them, applying the symmetry operators of R3m (#166), we can retrieve the 8 we had derived before (marked as “Table B” above), so they are equivalent in the low symmetry setting. But what about the remaining 6? Let’s take the 3rd entry \((0.27,0.53,0.63)\) and construct its orbit:
X_p = orbit_166[3] # Corresponding to (0.2667 0.7333 0.6333)
X_p[3] = 1
print("Position in subgroup basis: ",("{:6.4f} "*3)\
.format((*X_p.flatten()[:3])))
print("="*63)
print("Position in subgroup basis:")
positions_166_w_36op_x_rep = []
for t_x in range(2):
for t_y in range(2):
for t_z in range(2):
a = X_p + np.array([[t_x],[t_y],[t_z],[0]])
for op in ops_166:
ap = np.dot(op,a)
ap -= np.floor(ap)
ap[np.isclose(ap,np.array([1,1,1,0]).reshape(4,1))]= 0
ap[np.abs(ap)<1E-15] = 0
flag_not_found = True
for i in positions_166_w_36op_x_rep:
if(np.allclose(ap,i)):
flag_not_found = False
break
if(flag_not_found):
positions_166_w_36op_x_rep.append(ap)
for (i,wp) in enumerate(positions_166_w_36op_x_rep,start=1):
print(("{:2d}"+"{:8.4f} "*3).format(i,*wp.flatten()))
print("[Table D]")
Position in subgroup basis: 0.2667 0.7333 0.6333
===============================================================
Position in subgroup basis:
1 0.2667 0.7333 0.6333
2 0.2667 0.5333 0.6333
3 0.4667 0.7333 0.6333
4 0.7333 0.2667 0.3667
5 0.5333 0.2667 0.3667
6 0.7333 0.4667 0.3667
7 0.9333 0.0667 0.9667
8 0.9333 0.8667 0.9667
9 0.1333 0.0667 0.9667
10 0.4000 0.6000 0.7000
11 0.2000 0.6000 0.7000
12 0.4000 0.8000 0.7000
13 0.6000 0.4000 0.3000
14 0.6000 0.2000 0.3000
15 0.8000 0.4000 0.3000
16 0.0667 0.9333 0.0333
17 0.8667 0.9333 0.0333
18 0.0667 0.1333 0.0333
[Table D]
So, here we see that the entries #3-6 appear in the orbit of \((0.27,0.53,0.63)\) listed in the Table D above. And checking the 24 positions retrieved in Table A when we had generated by applying the transformed operators of Pm3m (#221) to the orbit elements of \((0.1,0.1,0.1)\) (in #221), we see that Table B + Table D counts for every site there.
Checking the Wyckoff positions of R3m (#166), we see that Table B is constitutes the 6c and Table D is the 18h positions. So our 8g position in the Pm3m (#221) space group actually split into 6c and 18h positions:
In other terms, even though the 24 sites were related to each other with respect to the operators of Pm3m (#221), this is no longer valid due to the loss of symmetry in R3m (#166). The orbit elements of 6c and 18h are still related with the other elements in their corresponding orbit but they are not related to the elements in the other orbits.
This is what Wyckoff Positions Splitting is. We will be using this fact in the future when evaluating the plausibility of possible transformation matrix connecting the supergroup \(\mathcal{G}\) to the subgroup \(\mathcal{H}\).
The relations and the splitting of the Wyckoff positions can also be inquired directly using the WYCKSPLIT tool of the BCS:
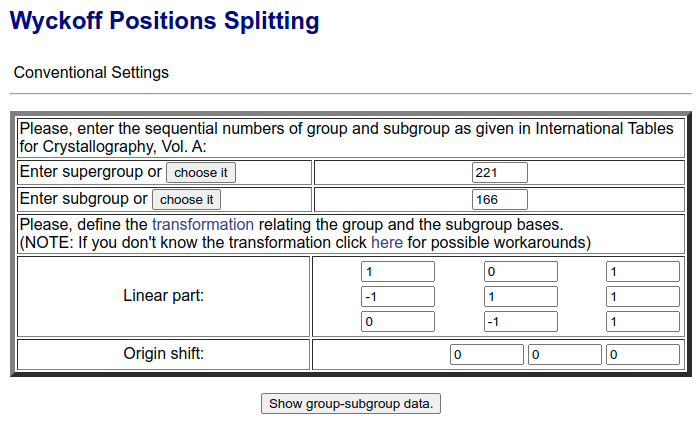

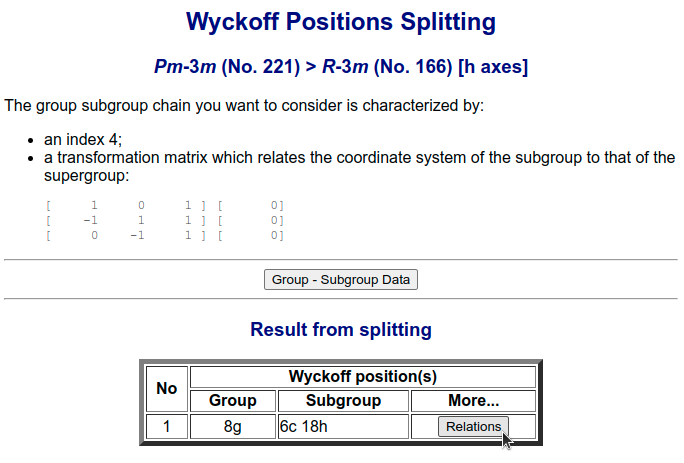
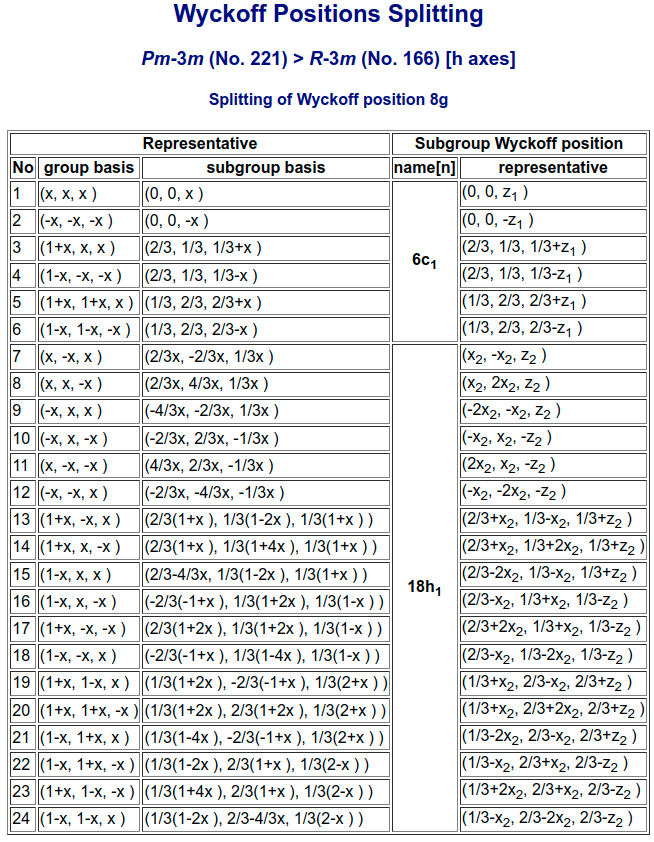
In this chapter, we have seen how to transform a structure given in high symmetry supergroup settings to a low symmetry subgroup settings using a transformation matrix. We have transformed the lattice parameteres (through the metric tensor), the symmetry operators and the site positions, and also learned how the Wyckoff positions can split due to the loss of some of the symmetries.
You can also use the TRANSTRU tool to directly transform a structure to a lower symmetry space group. Below, an example is worked out (with the ‘X’ site added to BaTiO3 to include Wyckoff position splitting):